Inductance
Summary: Excessive power bus inductance results in increased impedance and ringing in the Digital Command Control signal.
|
See the Video. |
Inductance and Impedance Reduction
Managing the impedance of your track bus is important. While this is an advanced topic, it is important to understand the basic principles to avoid creating problems when wiring.
In short, many of the issues outlined below can be resolved by 'Twisting Power Bus Wires and using the proper wire size.
A length of wire has impedance caused by the resistive and reactive properties of the wire. A larger gauge wire will have less impedance, as its resistance will be lower, and self-induction (reactive) properties are also reduced. The mathematics required to demonstrate this is complex and beyond the scope of The DCCWiki.
Three Steps to Managing Inductance
- Heavy gauge wire
- Avoid long runs
- Keep the pair of bus wires close together (AKA: Twisting).
It is important to understand that the reactive components of your wiring's impedance have an effect on phase relationships. Since a DCC signal is a pulse made from a fundamental frequency and its multiples (harmonics), as those relationships are altered by the reactive properties of the wiring distortion of the DCC signal results. This results in some frequencies travelling faster than others, distorting the pulse shape. Excessive inductance increases any ringing which may be present. By reducing the inductance, ringing is reduced.
Advanced Topic
The below items are advanced and it is not necessary to understand the physics involved. It is for reference.
Terms
- Inductance (Unit: Henry (H)) - The property of a wire to store current in the magnetic field around it, and oppose any change in the current.
- Impedance - A complex number consisting of the resistance and the reactance. This quantity is a vector, having both amplitude and a direction.
- Reactance - A property of inductors and capacitors, where their resistance varies with frequency, denoted by the symbol X. It is expressed as an imaginary quantity in calculations.
Impedance
In DCC, the impedance of the wire is important. The Reactive Component can be much larger than the resistive properties of the wire, controlling the Reactive Inductive component is important for good electrical performance of your wiring.
Impedance (Z) is calculated using the following formula: Z = √(R2 + X2)
- Where X is the reactive component, calculated as (XL – XC)
- XL is Reactive Inductance
- XC is Reactive Capacitance
- Frequency determines the Reactive component.
A length of wire will have impedance, caused by the resistive and reactive properties of the wire. A larger gauge wire will have less impedance, as its resistance will be lower, and self-induction (reactive) properties are also reduced. The mathematics required to demonstrate this is complex and beyond the scope of The DCCWiki.
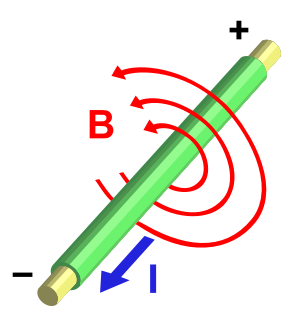
As the image shows, a magnetic flux surrounds the wire when current flows. The direction of the current determines the direction of the flux, as demonstrated by the "Right Hand Rule", where the thumb indicates current flow, the fingers wrapped around the conductor illustrate direction of flux.
Compare two long and widely spaced bus wires (inches apart) in parallel with two identical but closely spaced bus wires (~1mm apart). The latter have much less inductance, which is better. This is demonstrated in the table below. When a pair of wires make a long run parallel to each other, the one wire induces currents in the other. Since the two forces present are in opposition, they effectively cancel out. This was discovered in the early days of telephony. In fact, Alexander Graham Bell discovered that by twisting the two wires together, interference and inductance were reduced for a stronger signal and clearer communications.
Lenz's Law
"Nature abhors a change in flux." (D. J. Griffiths)
Inductance
A conductor in free space will have inductance when current flows through it.
Two properties of wire which impact inductance are gauge and length. Longer wires have increased inductance. Increasing the gauge (reducing the diameter) increases the inductance. To counteract the inductance of a long power bus, a heavy gauge wire should be used.
The impedance of the wire is dominated by the inductance. When the inductance is lowered, so is the impedance. A length of 10AWG has an inductance of 1.32µH, which at 8kHz results in an inductive reactance component of 66mΩ. The same length of wire has a resistive component of 3.3mΩ. The impedance (Z) computes to 66mΩ. This is why heavier wire is used than that of analog applications. A 14AWG wire has an impedance of 71mΩ for the same length. If the wiring loop is 5 times longer (10 in total) 10AWG is 660mΩ compared to the 710mΩ of 14AWG.
Voltage Drop: Many references to voltage drop and wire gauge ignore the physics in play, using the DC resistance to calculate the loss, ignoring that inductance and the resulting reactance has a larger influence than the resistance.
An effective method to decrease the inductance/impedance is keeping the wires close. The closer the better. The most effective solution is to twist the wires, with about three to five twists per metre. Doing so alters the phase relationships between the two wires, reducing any induced currents in the wire. Tying the bus wires together is also a very effective approach. Not only does it reduce the inductance, the increased capacitance reduces ringing in the bus. This is sometimes referred to as Closing the Loop. [1]
Attaching feeder wires to twisted bus wires gets complicated if one is not consistent with colour coding, however, if the wires are not twisted a great deal, it shouldn't be too difficult. Tying the two wires together with cable ties is just as effective, plus it is easier to connect feeders.
Self Induction
| Wire Properties | |||
|---|---|---|---|
| Length | 100cm | ||
| Frequency | 10kHz | ||
| DCCWiki.com | |||
| Gauge (AWG) |
Resistance | Reactance | Inductance |
| mΩ | mΩ | μH | |
| 22 | 54.1 | 101 | 1.6 |
| 20 | 33.3 | 98 | 1.55 |
| 18 | 20.9 | 95 | 1.50 |
| 16 | 13.2 | 92 | 1.46 |
| 14 | 8.3 | 89 | 1.41 |
| 12 | 5.2 | 86 | 1.37 |
| 10 | 3.3 | 45 | 0.71 |
Inductors store current in a magnetic field, when current flow increases, it resists that change. Lenz's Law states that a voltage, which will be opposite in polarity, opposes any increases in flux and current. This voltage is called Counter–Electromotive Force, or C–EMF, which is similar to Back EMF. This process is called Self Induction.
When the current decreases, such as when the booster output switches phase, the magnetic field collapses inducing an Electromotive Force into the inductor. When this happens the polarity of the self-induced voltage is reversed as the inductor attempts to maintain current flow using the polarity of the induced voltage such that it adds to the source voltage, raising the total voltage in an attempt to maintain current flow in the circuit.
Relays and solenoids do the same thing, which is why they have circuits added to prevent/reduce the damage the kick back can cause. As shown in the picture, a diode provides a path for the discharge current to flow when the voltage source is disconnected. Otherwise, the current would flow into the transistor and the microcontroller as it seeks a path. At the same time a large voltage spike would be imposed across the transistor. The diode clamps that voltage to about 1V, protecting the transistor and microcontroller.
Mutual Inductance
Mutual Inductance is the property where flux around one conductor induces a current in another. This is the principle by which transformers work. Mutual inductance can be additive or subtractive in nature.
By keeping the power bus wires close together, such as loosely twisting them, their mutual inductance reduces the total inductance. As k, the coefficient of coupling increases, the resulting inductance decreases, as per the formula:
- Total Inductance = L1 + L2 – 2M [2]
- Where M = k × √(L1 × L2)
- k is a value from 0 to 0.9. Perfect coupling is considered to be 0.9.
For example, if each bus wire were to possess an inductance of 50µHenries:
- k= 0.8 for a tightly coupled pair, LTotal = 20µH
- k = 0.4, for a loose coupling such as wires several inches apart, LTotal = 60µH
- With no coupling, (k = 0 the total inductance of the loop would be 100µH.
- The k values are just for illustration of the effect of mutual inductance and coupling effects.
Interference
At DCC Frequencies there is not much opportunity for interference with other electrical devices. While this is often given as a reason for twisting the bus, at the voltages and frequencies present the issue is not as great as many would believe.
Interference could be interpreted by multifunction decoders and could cause havoc on the system. This interference can come from outside the layout, or be caused by the bus wires themselves or nearby signal buses. Twisting the wires may reduce any interference the track bus may cause by inducing a signal in a low power signalling bus, such as your throttle network or occupancy detection system. It is also advisable to keep the various buses under your layout separated to reduce the possibility of mutual inductance. You don't want to induce signals in another bus, such as the throttle or LCC wiring. Also keep AC wiring away from your track bus and other layout buses.
Managing Inductance
This table demonstrates the differences that occur when the power bus wires are kept apart or close together.
The bus under test was made of two lengths of 12AWG wire placed in parallel, ~36 feet each for a total loop of ~72'. One end of the loop was closed to enable a reading to be taken.
- Before the inductance measurement, made with an Agilent ESR meter, each wire was measured, resulting in an Average impedance of each wire is 0.8Ω, L = 12.6μH, Resistance 0.09Ω. Measurements made at 10kHz to simulate DCC frequencies.
| Bus Wires | Z (Impedance, Ohms) | Inductance (μH) at 10kHz |
|---|---|---|
| https://dccwiki.com/Wire_Sizes_and_Spacing | ||
| Parallel, >1 foot spacing | 1.38 | 22 |
| Parallel, Tight | 0.57 | 9 |
| Loose Twist | 0.50 | 8 |
Referring the the illustration of the flux surrounding the wire: The right hand rule demonstates that in a DCC Power Bus, the flux in one conductor would have the opposite direction of the flux in the other conductor. Thus they would cancel out.
Video