Electronics Primer/Capacitors, Inductors and Resistors
The purpose of this acticle is to give an overview of the behaviour of various passive components in various circuits.
It is a work in progress.
Resistors
Reistors are the most basic of electronic devices. They are used to regulate current or reduce voltages as needed.
Resistors are measured in Ohms. See Ohm's Law for more details about resistance.
Resistors in Series
The total value of two or more resistors in series is the sum of the resistances:
- 100 + 100 = 200Ω
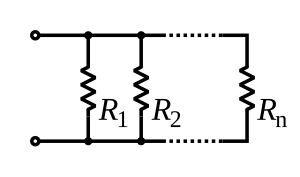
Resistors in Parallel
The total value of two or more resistors in parallel is less than the value of the lowest resistor: 100Ω || 100Ω = 50Ω
1/Rtotal = 1/R1 + 1/R2
or: Rtotal = 1/(1/100 + 1/100)
- 1/(0.01. + 0.01) = 1/0.02
- = 50Ω
- 1/RTotal = 1/R1 + 1/R2 … + 1/Rn
- 300||200||100 = ≈55Ω
A quick method which works for only two resistors is:
- Rtotal = (100 × 100) ÷ (100 + 100)
- = 10,000 / 200 or, by eliminating the zeros, 100/2
- = 50Ω
Capacitors
Capacitors and Inductors are Reactive devices, in that their behaviour is directly related to the frequency they operate at.
Capacitors are used much like resistors, to control currents based on their frequency. To direct current, a capacitor is an open circuit. To a 10kHz audio signal it may appear as a 200Ω resistor. These properties can be exploited to block a DC current from flowing while allowing the AC component to pass through.
Capacitors are measured in Farads
Series
In series, capacitors behave the opposite of resistors: The total capacitance of two equal capacitors in series is half their sum. For their working voltage, it becomes the sum of their working voltages.
Series: CTotal = 1/(1/C1 + 1/C2)
So, two 100µF capacitors in series would equal 1/(1/100µ +1/100µ)
- = 1/(10,000 + 10,000)
- 1/20,000
- 50µF
If these 100µF capacitors were 50WVDC (Working Volts DC), they would effectively form a 50µF, 100V capacitor
Parallel
Capacitors in parallel effectively create a larger capacitor by adding the surface areas of their plates together. The voltage does not increase.
So, two 100µF capacitors in parallel would equal 100 + 100 or 200µF
Reactance
Capacitors possess a reactive component, in that they will oppose changes. Their reactance, XC, is determined by frequency.
As the frequency increases, the capacitive reactance decreases. Generally, the bigger the capacitor the lower the frequency it works at. For example, a 100pF capacitor at 60 Hz has a reactance of 26.5MΩ. At 10kHz, that same capacitor has a value of 160kΩ. At 1MHz, it is now 1.6kΩ, and at 100Mhz it would be 16Ω. So what is effectively an open circuit at 60Hz would be almost a short circuit at 1GHz.
If that capacitor were changed for a 100µF capacitor, at 60 Hz XC would equal 26Ω.
Inductors
Inductors are measured in Henries. Inductors behave the same as resistors in series or parallel arrangements. Inductors are also known as Chokes or coils.
- Two inductors in series have a total inductance equalling the sum of the inductors.
- In parallel, the total is equal to 1(1/L1 + 1/L2)
Reactance
Inductors or chokes have the opposite behaviour of a capacitor. Inductors are wired to resist changes in the flow of current. They store the current in the form of a magnetic field, resisting increases in current while returning that energy when it decreases. They are often used in power supplies to smooth out any ripple in the current.
At 0Hz (direct current), their only property is the resistance of the wire it is wound from. Essentially it is a short circuit under those conditions. When an AC current is present, its behaviour changes.
For example a 1mH inductor has a reactance, XL, at 100Hz of 0.63Ω, at 1kHz it is 6.3Ω. Increase that frequency to 10kHz, and XL becomes 63Ω. This property can be exploited to allow a DC current to pass while blocking an AC signal.
There are two formulas for reactance:
- XC = 1/(2π FC)
- XL = 2π FL
Where F is frequency and the L or C represent the value of the inductor or capacitor. Note how the capacitor behaviour is the inverse of the inductor. When XL = XC, the circuit is resonant, and the impedance is almost zero.
LC Filters
As demonstrated, the properties of a capacitor and inductor can be exploited in various ways. Together they can form a filter to pass or block desired or undesired frequencies. Such as the crossover network in a loudspeaker which routes the bass frequencies to the woofer and the high frequencies to the tweeter. These circuits can range from complex circuits to a simple capacitor in series with the tweeter.