Ohm's Law

Summary: Ohm's Law describes the relationship between Resistance, Voltage and Current.

See the Video.

There is a good description of Ohm's Law on Wikipedia.

Ohm's Law

These examples apply to Direct Current.

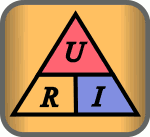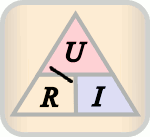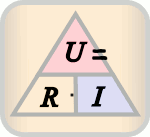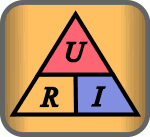
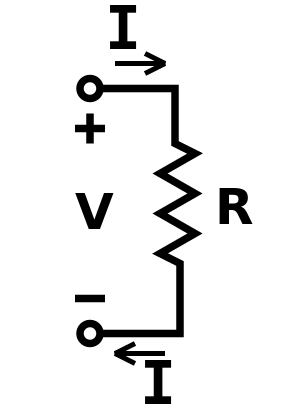
Ohm's Law is a statement of the relationship between Voltage, Current, and Resistance in an electrical circuit. It can be represented by this diagram:

Voltage may be represented by the letter E. This stands for "Electromotive Force," an older name for what is now called Voltage. Current is expressed with the uppercase I, as Ampere originally described it as "intensité du courant."

So, you may see the equations as:

• E = I × R (The animation below uses the European "U" for Voltage)
• I = E ÷ R
• R = E ÷ I

Examples

One common question is: "How much series resistance is needed for an LED?

To determine this, begin with the data sheet for the LED in question. Specifically, the values for the continuous forward current, I_FWD, and forward voltage V_FWD.

For example, the data sheet lists I_FWD as 30mA maximum, V_FWD at 20mA is from 3 to 3.6V.

The power source is 16VDC. The maximum voltage across the LED, V_FWD, is 3.6V. For safety, the V_FWD will be 3.3V. The series resistor (R_series) will be determined by the 3.3V at 20mA rating. R_series will have the difference between 16 and 3.3V across it.

V_Rseries = 16 − 3.3 = 12.7V

Using R = V ÷ I, calculate the value: 12.7 ÷ I_FWD = 12.7 ÷ 20mA

= 635 Ohms

• Using I = E ÷ R: 12.7 ÷ 635 = 0.02A
• Using E = I × R, 0.02 × 635 = 12.7V

There is no 635Ω resistor available on the market, so the closest value would be 680 ohms.

Using 680Ω, the current is 12.7 ÷ 680 = 19mA. Increasing the value to 750Ω reduces the current to 15mA.

Main article: LED Lighting and Resistors/Standard Resistor Values

Resistors in Series and Parallel

Series

Resistors in series

Total Resistance equals the sum of the resistances.

Parallel

Resistors in parallel

The total resistance of resistors connected in parallel is the reciprocal of the sum of the reciprocals of the individual resistors.

• 1/(1/R₁ + 1/R₂ … + 1/R_n)

When resistors are wired in parallel, the total resistance will be less than that of the lowest resistor's value.

Power Dissipation

The series resistor must be able to handle the power that will flow through it. Using the above calculations, the result is found as follows:

Voltage across the resistor is proportional to the current.

Watts = I² × R = 0.2² × 635 = .0004 × 635 = 0.25 W

In this case, a ¼W resistor or better will suffice.

Ohm's Law Explained

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

If you don't know Ohms Law, then you are missing out!

See Also

Electronics Primer